今天,我们先来看一个数学题,所有正整数无穷相加,即1+2+3+4+5+……,它的值是多少呢?也许有观众朋友说,虽然我无法一下子给出答案,但是按照常理推,这个结果应该是一个非常大的数字。
不过呢,在数学界中一旦涉及到无穷,就和物理学进入量子力学一样,一切都不能用正常思维去思考了。1+2+3一直加到无穷最后的结果竟然是-1/12。而给出这个公式证明的人,就是我们今天故事的主人公,被称为从未来穿越而来的天才数学家拉马努金(Srinivasa Ramanujan)。
拉马努金为什么算天才呢?因为他从小没有受过正规的训练,却表现出了异于常人的数学天赋,仅凭“直觉”就能写下极其复杂的数学公式。在他短暂的一生中,拉马努金留下了将近4000个公式及命题,由于他没给出证明过程,所以当时没有人能看懂这些公式。在很多年之后,数学家们才解开了其中的一些公式命题,甚至由此获得重大数学成就。比如,比利时数学家德利涅(V. Deligne)在1973年证明了拉马努金1916年提出的一个猜想,并因此获得了1978年的菲尔兹奖,而这是世界上最高的数学奖荣誉。
那为什么又说拉马努金是穿越而来的呢?因为当代科学家在研究他那些神秘的公式时,赫然发现,他写下的好几个定理涉及到粒子物理、统计力学、计算机科学、密码技术和空间技术等不同领域。而1919年,在拉马努金生命的最后一年,他写出的最后一个公式,到2012年才被人破解,数学家表示这一函数可以用来描述黑洞的行为,要知道,当拉马努金首次提出这种函数的时候,人们连黑洞是什么都还不知道呢。
拉马努金的伯乐、导师兼好友,英国大数学家哈代(G. H. Hardy)曾表示自己一生对数学领域最大的贡献就是发掘了拉马努金,他还感叹,“我们是在学习数学,而拉马努金则是发现并创造了数学。”
而拉马努金也不止一次地向哈代表示,甚至证实他的数学天赋来自于神,这一切也都深深震撼着持有无神论观点的哈代。
下载点选后右键单击 "另存新檔"
天才出世
1887年12月12日,在印度埃罗德(Erode),一个远离邦首府马德拉斯(Madras)的小镇,有一个男孩降生了,家人为他取名叫拉马努金。埃罗德是一个很贫穷的小镇,即便拉马努金的家族属于印度种姓制度中最高等级,他们家还是相当贫穷,全家人就靠父亲每月的工资20卢比生活,日子过得紧巴巴的。
小拉马努金并不像一些天才儿童,三四岁就展露头角,他的才华直到1898年,他十岁的时候,才逐渐被发现。那一年,小拉马努金进入了一所学校读书,第一次接触到正规的数学。而这时,他的家里也住进了两个房客,时不时也教小拉马努金一些数学。等拉马努金11岁时,这两位房客已经感到自己的数学能力已经教不了这个孩子了,而这两位房客也不是一般人,他们是当时政府大学的大学生。
拉马努金12岁时,高班的同学借给他一本朗内(S. L. Loney)写的《平面三角学》(Plane Trigonometry)。令人惊讶的是,拉马努金在短时间里自学完整本书,不仅解答出书中所有的问题,还独立推导出欧拉公式(Euler’s formula)。
拉马努金进入高中后,一次在学校图书馆中他借到了英国数学家G‧S‧卡尔(George Shoobridge Carr)的《纯粹及应用数学的基本成果概要》(A Synopsis of Elementary Results in Pure and Applied Mathematics)一书。这是一本让一般人头大的数学著作,里面包含着代数、微积分、三角学和解析几何的5000多个公式,但没有给出详细证明。然而,拉马努金却爱不释手,最后用自己的方式,把所有的公式都证明了一遍。
拉马努金因为数学成绩优异曾获得奖学金,然而他偏科太严重,除了数学,他什么也不感兴趣。结果,到学期末他因为英语等成绩太差而失去奖学金,并最终因为文科成绩不合格而被迫辍学。
穷困潦倒中的磨砺
离开学校之后,拉马努金继续过着贫困的生活。1909年,他结婚了,按照传统他必须得外出谋生养家了。拉马努金找到印度数学学会的创始人之一艾亚尔(R. Aiyar),请他给自己一份糊口的差事。是金子总是会发光的。拉马努金后来被推荐给印度数学学会的另一位创始人拉奥(R. Rao)。拉奥爱惜拉马努金的才华,表示愿意按时给拉马努金一些钱,维持他一段时期的生活,同时向有关方面为拉马努金争取研究津贴,以使他能安心从事研究。
然而,孟子说过:“天将降大任于斯人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身。”拉奥为拉马努金申请的津贴没有拿下来,而拉马努金也很有志气,不愿意成为别人的经济包袱,也很长时间不去拉奥那里领钱了。因为没钱买纸,拉马努金都是在石板上做数学演算,然后直接用胳膊肘去擦,时间一长,胳膊肘被磨得又黑又厚。
生活还得继续啊,好在拉奥等人是真心愿意帮助这个有才华的年轻人,他们帮拉马努金在金奈(Chennai),原名叫马德拉斯(Madras)的港务局找到一份工作,月薪25卢比。虽然薪水不多,但总是可以解决温饱问题了。于是,拉马努金把精力投入在数学研究中,并开始初步崭露头角。
他在著名的《印度数学会杂志》(Journal of the Indian Mathematical Society)上发表了一些论文,在印度的数学圈渐渐有了名气。因为当时英国的数学研究做得很好,于是有人就建议拉马努金联系联系英国的数学家。
仔细思考之后,拉马努金给英国剑桥大学的几位著名数学家发了一份一模一样的信。
大洋彼岸的神秘来信
1913年的一个冬日,英国剑桥大学三一学院的数学教授哈代在吃完早饭之后,按照惯例拿起桌边的《泰晤士》报纸,准备了解当日新闻。这时,报纸上放着的一封信引起了他的注意。信封上贴着来自印度的邮票,并写着“马德拉斯,1913年1月16日”。虽然自己似乎在印度马德拉斯没有熟人,哈代还是打开了信封,抽出了长达10页的信。
作为著名的数学家,哈代经常收到这类毛遂自荐的信,然而拉马努金的信让他颇为惊讶。整封信除了几句英语介绍之后,完全就是用代数、三角函数、微积分这样的数学语言写成的。满眼的公式啊,估计哈代都要看晕了。
当天晚上,哈代找来了他的好友,也是著名数学家李特尔伍德(J. E. Littlewood)一起研究这份信。从晚上9点到凌晨12点,三个小时过去了,他们俩竟然都没有完全看懂信中的公式。但是有一件事他们已经清楚了,就是这个写信的人一定是个数学天才。
哈代兴奋地向拉马努金发出邀请,并为他申请了丰厚的奖学金。然而,拉马努金这边却迟疑了,因为他的家人担心他一旦出国就会失去在印度的高贵种姓。直到有一天,拉马努金的妈妈在睡梦中梦到神告诉她,不要阻挡儿子的前程,这样她才下决心让儿子出国。
天才的鼎盛时期
来到英国之后,拉马努金在哈代和李特尔伍德等人的帮助下,学习了很多数学的基础知识,以及正规的数学研究方法,在欧洲的5年里,他在英国、法国、德国的数学杂志上共发表了21篇论文。
在拉马努金与哈代合写的一篇论文中,他们对困扰数学家多年的整数分拆问题作出了惊人的解决,首创了正整数n的分拆数p(n)的渐近公式。
这里稍微介绍下正整数拆分,就是对于一个正整数n,它可以有1个或多个正整数叠加而成,p(n)就代表了不同的叠加方式。
比如:1=1, p(1) =1
2=2, 2=1+1, p(2)=2
3=3, 3=1+1+1, 3=1+2, p(3)=3
4=4, 4=1+1+1+1, 4=1+1+2, 4=1+3, 4=2+2, p(4)=5
……..
我们这里也展示下拉马努金和哈代的公式:
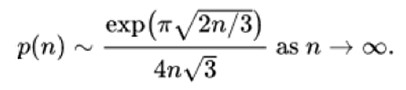
凭借着这个公式,拉马努金于1918年被推选为英国王家学会会员,这是英国数学界的最高荣誉,而拉马努金也是有史以来最年轻的会员。
哈代对于拉马努金的才华非常欣赏,他在自己设计的一种关于数学天才的非正式的评分表中,给自己评了25分,给好友兼数学家李特尔伍德评了30分,给他同时代最伟大的数学家希尔伯特(D. Hilbert)评了80分,而他给拉马努金,评了100分。
他时常对拉马努金写的公式赞不绝口,问他:你是怎么写出来?而拉马努金则常常简单地回答道:这是神在梦中指点给我的。拉马努金自己说,在睡梦中他的思路就会变得很清晰,能够接受到海量信息。在梦中,神在墙上写下一个又一个公式,他记住那些公式,醒来后,把公式记录在笔记本上。
一开始,信仰无神论的哈代以为拉马努金是在逗他玩呢,然而一次又一次,拉马努金在睡醒觉之后,就给出了令他们头疼的难题的答案,让哈代着实吃惊不已。看着拉马努金那三大本笔记本,上面写满了超级复杂又没有证明过程的公式,哈代逐渐相信,拉马努金确实有不同于常人的特殊能力,他或许真的能和神沟通。
哈代很高兴自己发掘出了天才拉马努金。然而,他们快乐的合作生活只维持了三年。
最后的时刻
拉马努金如痴如醉地把一切精力投入到数学研究之中,经常忘记吃饭,忘记休息,他的身体时常出现疼痛,最后在1917年发现他患上了肺结核,他在英国的最后一年,几乎都是在疗养院度过的。然而,在病床上,拉马努金还是在想着数学。
这里还有一个小插曲。有一天,哈代乘坐一辆出租汽车去疗养院看望拉马努金。哈代对拉马努金说:“我搭计程车来,车牌号码是1729,这数字真没趣,希望不是不祥之兆。”拉马努金想一下马上回答:“不,这个数有趣得很。在所有可以用两个立方数之和来表达,而且有两种表达方式的数之中,1729是最小的。”即1729=1^3+12^3=9^3+10^3,后来这类数称为的士数。难怪,哈代会发出感叹:“每个数都是拉马努金的朋友。”
久病没有好转的拉马努金思乡心切,在1919年回到印度,然而这并没有让他好起来,转过年来的4月,拉马努金病逝,当时他只有33岁。他一生清贫,死后仅留下两张照片,以及一个热敷用的热水袋和一些书籍文稿。
拉马努金在病床上,还留下了第四本记录公式的笔记本,这本笔记本被称为“遗失的笔记本”,因为在他死后50多年一直都不知下落。直到1976年,美国宾夕法尼亚大学教授G‧安德鲁斯(G. Andrews)访问剑桥大学三一学院时,在该校的图书馆中发现这本笔记本,上面有600多个没有证明过程的公式。
当现代的科学家研究拉马努金的这几本手稿时,发现它们如同一个巨大的宝藏,蕴含着众多难以揭开的奥秘。拉马努金的一些公式在众多尖端科学领域起着重要的作用,甚至隐藏着黑洞的秘密。
拉马努金一生坚信,他的数学灵感来自于神,或许也只有这样才能解释,为何他能有如此超凡的成就。拉马努金的故事,后来在2015年被拍成电影《知无涯者》。据说,数十位硅谷科技领袖在一次宴会中一起看了这部电影,很多人最后红着眼眶走了出来。
好了,今天就和大家分享到这里,未解之谜,我是扶摇,我们下期再见。
欢迎订阅Youmaker频道:https://www.youmaker.com/c/UnsolvedMystery
订阅频道YouTube频道:https://www.youtube.com/channel/UCzvQZ1p_-AXgAWiyHhE7CxQ
订阅未解之谜Telegram群组:https://t.me/wjzmchannel
【未解之谜】节目组制作
大纪元 / 原文网址:https://www.epochtimes.com/gb/22/3/17/n13653509.htm















